Just show you what i'm study today while i'm doing my revision,
The Laplace transform of a function f(t), defined for all real numbers t ≥ 0, is the function F(s), defined by:
The lower limit of 0 − is short notation to mean 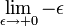 and assures the inclusion of the entire Dirac delta function
and assures the inclusion of the entire Dirac delta function 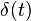 at 0 if there is such an impulse in f(t) at 0.
at 0 if there is such an impulse in f(t) at 0.
The parameter s is in general complex:
This integral transform has a number of properties that make it useful for analysing linear dynamical systems. The most significant advantage is that differentiation and integration become multiplication and division, respectively, with s. (This is similar to the way that logarithms change an operation of multiplication of numbers to addition of their logarithms.) This changes integral equations and differential equations to polynomial equations, which are much easier to solve.
The Laplace transform is named in honor of Pierre-Simon Laplace, who used the transform in his work on probability theory. The Laplace transform was discovered originally by Leonhard Euler.
And some more this only the introduction.....bbbbbaaaaaadddddd...
So, if you are interesting or going for engineering course, better consider it carefully, else you will feel like me one day... Good day!!!

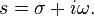
No comments:
Post a Comment